ゆらぎの世界へ
アインシュタインの2つの論文により、私たちの世界に対する見方は一変した。宇宙の果てや運命を支配する相対論、ミクロの極限へと向かう量子論により、時空のデザインが私達の前に広がったのだ。
しかし、相対論というマクロの世界と、量子論というミクロの世界のはざまの世界を私達は理解したのだろうか。はざまの世界は絶え間ない「ゆらぎ」にさらされる世界でもある。たなびく雲、風に舞う一片の雪、そして生まれては逝く生命、このような世界を語る言葉を物理学は持っているのだろうか。まさに、アインシュタインの言ったように、知れば知るほど分からないことの多さを知らされるのだ。だが、アインシュタインはそこに第3の扉を用意していた。他の論文に比べて、一見地味に見える3つめの論文、ブラウン運動の論文は「ゆらぎ」の世界へ私達をいざなう扉でもあった。ブラウン運動は、粒子の運動である。例えば、たなびく雲を思い出してみよう。雲は、たくさんの水や空気の粒が揺れ動く中で生まれては消える。アインシュタインの第3の論文を出発点として、絶え間ない変動と不安定にさらされる世界(非平衡状態)を扱う物理学が生まれた。無数の分子が存在する私達の世界には、一個一個の分子の運動からは予測がつかない偶然性や規則性があり、異なった法則に支配されている。それらを理解するためには、移り変わりの中に法則を探り、数学的な記述方法を見出す物理学(非平衡物理学)が必要であった。非平衡物理学の一つの流れは、線形応答理論に発展し、電気抵抗と熱雑音の理論的関係や、磁性体など様々の物質の物性を予測する基本理論として、通信やコンピュータなど現代のあらゆる技術に用いられている。もう一つの流れは、不安定性を捉えるカオス理論や構造形成の理論へと発展した。不安定性は、ゆらぎを拡大するため、同じ方程式に支配される場合でも、異なった結果を生み出し、世界に多様性を与える原因となっている。この分野は現在では、生物の形態形成のメカニズムや、私達の筋肉の動きとそのエネルギー効率の問題さえも研究対象としながら発展を続けている。また、ブラウン運動の軌跡が持つ、拡大を繰り返しても同じ構造が見えてくる性質は、フラクタルという数学の概念をつむぎだし、自然科学だけでなく、経済やデザインの世界でも使わるようになっている。「ゆらぎ」の世界の物理学は、このように現代の物理学を生き生きとしたものにしている。
雲もフラクタル |
|
ブラウン運動をめぐる歴史 |
植物学者ロバート・ブラウンは、1828年に水面に浮かんだ花粉の粒子がひとりでに動き回ることを発見した。花粉から出た1ミクロンくらいの粒子を顕微鏡で観察すると、ピコピコと激しく動き回っているのが見出された。彼は当初、これを有機物特有の性質と考えたが、その後、ガラスや岩石のかけらなど無機物でもこの運動は観察され、しかも時間がたっても一向に衰えないことを発見した。これはブラウン運動と呼ばれるようになり、19世紀の科学界に話題を巻き起こした。
物質が原子・分子からできていると考える原子論者は、水の分子が花粉の粒子に衝突することによりこの運動が引き起こされると考えた。熱現象が分子の運動によって生じるとする分子運動論から予想されたことは、気体中の分子も水の分子も秒速数百メートルというすさまじい速さで動いているということだった。それらの分子が絶え間なく花粉粒子に衝突することによってブラウン運動が引き起こされるとする説が19世紀後半には発表された。見積もりによれば、水の分子は、1秒間に1千万回も粒子に衝突する。しかしあまりにも多くの分子があらゆる向きから衝突するため、それらの力は互いに打ち消されその結果、粒子は水の分子より遅い速度で動き回ると考えられた。
分子運動論によれば、全ての分子の運動エネルギーは等しく分配されると予想される。もしこの理論が正しければ、花粉の粒子でさえも分子一個と同じエネルギーを持つはずであると予想された。しかし、粒子の速度から運動エネルギーを見積もると理論から予想されるものより、7〜8桁も小さな値となるため原子論の正しさを示す証拠にはならなかった。実は、ブラウン運動の軌跡は精度を粗く測定するほど遅くなり、精密に測定するほど早くなるというフラクタルという性質を持っており、当時の測定精度では速度の正確な測定は不可能であった。
アインシュタインは、ブラウンの結果を知らずに1905年に論文を書き、粒子の拡散や分布という測定しやすい長時間の振舞いを測ることにより、原子の存在を実証できると予想した。また、逆にこの理論が実験で否定されれば、分子運動論にとって大打撃となることも指摘していた。ジャン・ペランは、1906年にアインシュタインの予想に基づきブラウン運動に関する注意深い実験を行い、アインシュタインの理論の正しさを実証した。様々の方法から見積もられた分子の数(アボガドロ数)は、プランクが黒体放射の理論から予測した数値ともほぼ同じ値となり、ブラウン運動の観察は物質が原子からなっているということを確証する実験となった。
水に落としたインクが拡散してゆく現象も、インクの粒子がランダムなブラウン運動をしながら全体として分布が広がってゆく結果と見ることができる。アインシュタインは、簡単な理論によりこの広がり方を予測し、一方で重力と拡散のつりあいで決まる粒子の分布を予測し、その2つの結果からアボガドロ数が見積もれると結論したのだった。
粒子の分布が広がる早さをあらわす拡散定数と、粒子に外力を加えたときの抵抗の逆数が比例するという関係式は、アインシュタイン関係式と呼ばれ、現在では、コンピュータの主要部品である半導体の理論を初め、現代の科学技術のあらゆる場面で役立っている。 |
|
アインシュタイン関係式と非平衡の統計力学
アインシュタインがブラウン運動の考察から導いたアインシュタイン関係式は、その後、非平衡統計力学という研究分野を生み出し、今また新たな展開の時期を迎えている。
アインシュタインとペランは、小さな粒子の運動をつぶさに追いかけることにより、原子の存在を実証した。熱力学は熱現象をマクロに扱う学問であり、当時すでにゆるぎないものであったが、これをミクロの分子運動から導こうとする統計力学はアインシュタイン等の功績により確固たる基盤を得たと言ってよい。その後、統計力学は量子力学を取り入れ、固体の比熱や黒体輻射の問題も解決し、一見完成したかに見える。しかし、統計力学は実は限られた条件でしか成り立たないという大きな制約を持っている。
温度などが一定、一様で熱や物質の流れがない状態を熱平衡状態と呼ぶが、熱平衡状態を扱う平衡熱力学や平衡統計力学は上の意味で完成したと言える。しかし、熱平衡状態はそれ以上変化しない、いわば死の状態であり、生き生きとした状態は熱や物質が流れて、絶えず変化している状態で始めて現れることができる。この非平衡状態を扱うことができないということが平衡統計力学の限界であった。非平衡状態に関する研究はその後徐々に発達してきたが、1950年代の日本において大きな発展がもたらされた。アインシュタインのブラウン運動に始まるこの理論は線形応答理論と呼ばれている。
ここで平衡状態の周りのゆらぎについて述べておこう。小さな粒子は常に水分子の衝突を受け、それらの力が完全に打ち消されないためにブラウン運動を示した。ブラウン粒子も周りの水を含めれば温度が一定の熱平衡系である。同じように、小さな熱平衡系は常にゆらいでいる。電気抵抗の熱雑音も同じ理由で電子の運動のゆらぎが電圧や電流のゆらぎとなって表れたものである。抵抗の熱雑音は電気的ノイズの主な原因であり、通信やコンピュータの発達とともに常に大きな問題となっている。ブラウン運動においては、粒子運動のゆらぎが大きければ拡散も早い。アインシュタインの関係式は、ゆらぎの大きさと外部から力を加えた時の動きやすさが比例していることを示していた。実はこの中に平衡状態を離れて非平衡状態を考えるためのヒントが埋め込まれていたのである。平衡状態から少しずらすためには、外から力を加えればよい。一般に加えた力が弱ければ応答としての動きの速さは比例する。これを線形応答と言う。電気回路の経験則であるオームの法則は、外部から加えた電圧に比例して電流が流れることを示しているが、これが線形応答の簡単な例である。では電流の流れやすさ(抵抗の逆数)はゆらぎの大きさとどう関係するのか、外力をかけたときの応答の仕方とそれはどう結びつき、力学や量子力学からどう導けるのかが当時の非平衡統計力学の大きな課題であった。
久保亮五(1910-1995)や富田和久(1920-1991)の磁気共鳴の理論は、この問題に深く関わっており、その後、中野藤生(1922-)の電気伝導の場合の定式化を経て、久保(1977年ボルツマン賞)が線形応答理論として一般化を行った。これらは現在、久保公式と呼ばれ、半導体を始めとする物性の分野や磁気共鳴画像装置(MRI)などの医療画像診断まで基礎、応用を問わず重要な基本公式として広く用いられている。 |
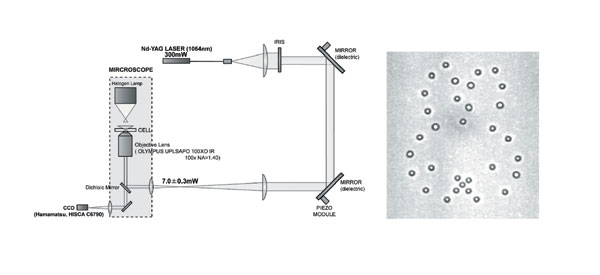
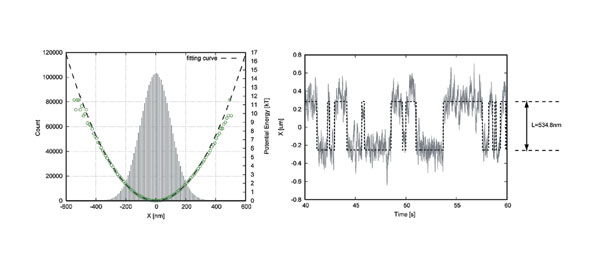
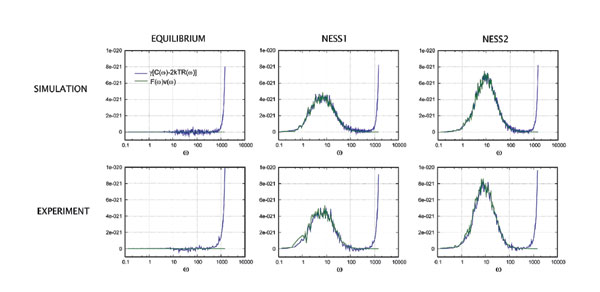
アインシュタイン関係式と非平衡の熱統計力学 |
線形理論を超えて
ある種の物質では線形の範囲を超える強い電圧が加わると、かえって電流が沢山流れ易くなることがある。一般に非平衡状態では外からエネルギーを注ぎ込むと、外からの力とそれに対する応答が比例関係でなくなり(非線形応答)、一気に別の振る舞いをする場合があるのだ。そこではアインシュタインの関係式は破れてしまう。その時、ゆらぎはどのような法則に従うのだろうか。アインシュタインがブラウン運動の考察から導いたアインシュタイン関係式は、その後、非平衡統計力学という研究分野を生み出し、今また新たな展開の時期を迎えている。
コーエン(2004年ボルツマン賞)等は、非平衡定常状態でゆらぎの分布が従うべき新しい「ゆらぎの定理」を発見した。「ゆらぎの定理」は、その特別な場合として久保公式を含んでおり、線形領域を超えても成り立つことが知られている。さらに2005年になり、原田崇広(福井大)と佐々真一(東大)は、アインシュタイン関係式の破れの大きさがミクロなシステムの発熱に一致するという新たな関係式を見出した。そしてこの関係式が正しいことがごく最近、我々のグループの実験により検証された。この関係式は、生物物理の分野などでも役立つことが期待されている。私達の筋肉を作っているタンパク質分子も絶えず無数の水分子の衝突を受け、ブラウン運動をしながら力を出していることが最近の実験で確認されている。筋肉を動かすこれらの分子は分子モーターと呼ばれている。分子モーターの運動の解析やエネルギー効率の理解のためにも非平衡統計力学が使われ始めている。 |
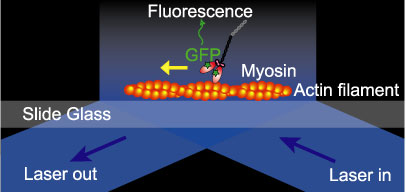
全反射照明を用いた1分子イメージングの模式図 |
|
ブラウン運動とフラクタル
雪の結晶は美しく、一つとして同じものはない。あの美しい構造はどのようにして作られ、多様性はどうして生まれるのだろうか。そこにブラウン運動が深く関わっている。ここではブラウン運動が作り出すフラクタルパターンについて述べよう。
図1はブラウン運動の軌跡を表している。ブラウン運動の測定から、原子・分子の存在を実証したジャン・ペラン(1926年ノーベル賞受賞)は、粒子の軌跡を30秒ごとに観測したスケッチを残している。30秒ごとの粒子の位置の間は、直線で結ばれているが、この直線にさしたる意味はない、なぜなら、測定の時間間隔を1秒ごとにすれば、直線は直線でなくなり、さらに細かく折れ曲がった直線の集まりとなる。人間の目では10分の1秒程度の変化を見るのが限界だが、高速度カメラでは、10000分の1秒の分解能で観測することも可能だ。それでも粒子の軌跡は複雑に折れ曲がっている。この性質のために、粒子の速度を正確に測ることは難しい。測定された速度は、分子運動論のエネルギー等分配則が予想する値より7〜8桁も小さな値となってしまうことが、原子論者を悩ませたのだった。このように拡大しても拡大しても同じような構造が繰り返し現れる幾何学図形を現代ではフラクタルと呼んでいる。フラクタルの名付け親であるマンデルブローは、ブラウン運動の軌跡の長さは、拡大すれば際限なく増大すると述べている。 |
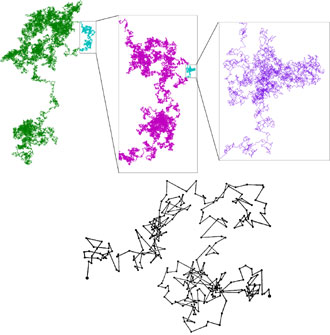
図1 |
アインシュタイン自身も、1905年の論文の中で、ブラウン粒子の軌跡を、過去の記憶を持たない軌跡、したがって微分不可能とみなしている。そのため個々の運動を解析せずに統計平均としての拡散現象の解析を行っている。しかし、微分不可能な曲線という考えは、長い間、数学者の頭を悩ませ続けることとなった。
ペランもイギリス海岸の長さを測ることは難しいと述べているように、自然界には複雑で長さや面積が決め難い図形はたくさん存在する。ここで簡単な図形を例にとり、フラクタル図形の長さを測定することを考えてみよう。
図2は、コッホ曲線と呼ばれる図形の作り方を示している。(a)のように長さ1の線分を用意する。(b)にように直線の真ん中の1/3を取り除き、そこに一片の長さが1/3の正三角形の2辺を乗せる。次に(c)のように各直線の中心の1/3を取り除き(長さは1/9)、替わりに正三角形の2辺を乗せる。この操作を次々と無限に繰り返して得られる図形が仮に(d)のように書けたとすると、その図形はコッホ曲線と呼ばれ、フラクタルな図形である。この曲線の長さは、付け加えていった線分の長さを足し合わせると無限大となる。
|
|
しかし、この図の印刷のように現実の観測には限界がある、長さを測る物差しにも最小単位が存在する。最小目盛りが1の物差しで測れば、コッホ曲線の長さは約1としか測れない。最小目盛りが1/3であれば、曲線に沿って物差しを4回当てて測ることになるので長さは(1/3)x4となる。目盛りが1/9=(1/3)2まであれば、物差しを当てる回数は、42回となり、長さは(1/3)2x42となる。一般に目盛りが(1/3)nのとき、回数は4n、総延長は(1/3)nx4nとなるので、nが無限大のとき長さも無限大になる。一方、長さが無限大の曲線はいくらでも作ることが可能だ。4個という個数を変えることで様々の長さ無限大の図形ができあがる。このとき、図形の違いを区別するものは何だろうか?その指標の一つがフラクタル次元である。フラクタル次元は、次のように定義される。 |

図2 |
つまり、フラクタル次元は、物差しを細かくしていったときに長さが長くなる度合いを表す量と言ってよい。今の例に適用すると、フラクタル次元は、D=ln4/ln3〜1.26となる。曲線の次元は線であるかぎり1次元であるが、フラクタル次元を導入することにより、複雑さの度合いを数値化し分類することが可能となる。
この考え方でいくとブラウン運動する粒子の軌跡のフラクタル次元は2次元となる。アインシュタインは、時間tの間にブラウン粒子が移動する平均距離は、時間の1/2乗に比例すると予測したことを思い出そう。物差しの最小単位を観測する時間間隔と考えて、時間間隔を1/2にすれば長さは4倍になる、したがって、フラクタル次元は2となる。ブラウン運動は1次元の曲線でありながら平面を埋め尽くすフラクタル図形になっているというわけである。
さて、次にブラウン粒子が多数集まって出来るフラクタル図形を紹介しよう。ブラウン運動は、ランダムウオークまたは酔歩とも呼ばれるごとく、確率的でランダムな運動である。計算機でランダムウオークを生成するのはやさしい、マス目の上に置かれた粒子に対して、毎時刻にサイコロを振り、次に東西南北、どちらの方向に動くかを当確率で選ぶことを繰り返すだけである。図3(a)の軌跡は、そのようにして作られたランダムウオークの例である。このとき、中心に1点、凝集の種となる動かない粒子を置いておこう。ランダムウオークでやってきた粒子がたまたま、この中心の種に衝突するとくっついて動かなくなるものとする。さらに次のブラウン粒子がやってきて、すでに凝集した粒子のどれかにくっついたらまた動かなくなる。粒子は中心から十分離れてあらゆる方向からランダムにやってくるものとする。また、くっつくことなく遠くにさってゆく粒子ももちろん存在する、しかしこのようにして次々とランダムウオークと凝集を繰り返すと中心の種を核として、粒子のクラスターが徐々に成長してくる。その結果、得られたパターンが、図3の(b)である。 |
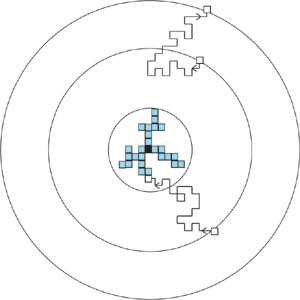
図3(a) |

図3(b) |
これほど単純なシミュレーションが図3のような複雑なフラクタルパターンを生み出すことは大きな驚きである。このパターンは、拡散によって律速された凝集パターンという意味で、DLA(Diffusion Limited Aggregation)と呼ばれる。多くのグループにより大規模なシミュレーションが行われ、2次元空間で成長したDLAのフラクタル次元は1.71であることが明らかになった。また、3次元で成長すると2.5次元となることや、一般化して10次元の空間における計算まで行われた。
拡散は数学的には、粒子の濃度分布が時間に対して1階微分、空間に対しては2階微分の項をもつ拡散方程式で記述される。今のようにゆっくりした成長では、時間変化は遅いため無視でき、濃度の空間2回微分=ゼロというラプラス方程式によってブラウン粒子の空間分布は記述される。本来、滑らかな数学的な解を持つと思われ、物理の至る所で顔を出すラプラス方程式から、これほど複雑で微分不可能な図形が現れることが1991年に発見され、数理や物理の世界に驚きを持って迎えられたのである。 |

図4(a) |
しかも、わずかその2,3年後にコンピュータシミュレーションではなく、実験においてもDLAが発見された。自然界のフラクタルでなおかつ成長メカニズムと基礎方程式が特定できる系として、DLAは最も現実的なフラクタルパターンとして認識されるようになったのである。図4は、様々の実験系で観察されたDLAのフラクタル構造である。(a)(b)は、金属葉と呼ばれる金属イオンの析出や電気メッキで現れる多結晶の凝集パターンであり、(c)は、放電で現れるパターンである。また、しのぶ石と呼ばれる岩石の表面に析出した樹枝状のパターンやバクテリアのコロニーでさえDLAと一致することが分かっている。 |

図4(b) |
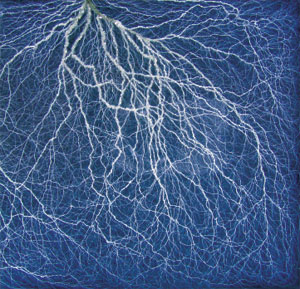
図4(c) |

図5(Fractal Forms(ElseVier/North-Holland_1991)plate32.) |
現在では、DLAパターンは、拡散方程式で支配される成長パターンに共通して現れる普遍的なフラクタル構造であると理解されている。自然界には、様々のフラクタルがあり、その成因も形作る物質もことなるが、成長のメカニズムがDLAであれば、そのフラクタル次元は、2次元では普遍的に1.7次元となることをこの結果は意味している。また、逆にフラクタル次元が1.7であれば、その成長メカニズムは粒子の拡散過程によって決定されている可能性がある。
さて、雪の結晶の多様性はどこから生まれるのだろうかという疑問に戻ろう。上で述べた金属葉の成長やビスカスフィンガーの成長パターンは結晶成長と深く関わっている。ビスカスフィンガーの成長の際に、底面のガラス板に溝をつけ、特定の方向に枝が成長しやすくしたときに現れるパターンが図5である。全体として六角の対称性を持ち、雪の六華構造と極めて類似している。伸びやすい方向を与えたことによる秩序と枝が成長する際の不安定性が競合したことによりこのような美しい構造が生まれる。六華模様で知られる雪の結晶は、気相中で水蒸気が何らかの核に向かって凝集した結果作られる結晶構造である。水分子の強い相互作用で結晶成長は特定の方向へ伸びやすくなり秩序が形成される。そのため、ブラウン運動のゆらぎが作り出すランダムさは打ち消されてしまう。一方、過冷却状態では、結晶の枝先端の成長速度が速いため、不安定性が起こり、側枝が次々と形成される。この枝分かれの様子は、不安定性のためにミクロのゆらぎが拡大されパターンの多様性となって表れる。実は雪の結晶の形は、ブラウン運動、DLA、秩序形成、不安定性の全てが関わっている興味深い現象なのだ。 |
|
非平衡系の物理学(構造形成とカオス)
注:)実は日本の科学の創成期において、寺田虎彦とその門下の研究者達が、
非平衡物理の源流ともいうべき研究を行っていたことは良く知られている。
寺田は、上記で述べた構造形成の問題の多くを「自然界の縞模様」などの随筆で述べている。
また、寺田の弟子である中谷宇吉郎は人工雪の研究や雪の中谷ダイアグラムなどで知られている。
非平衡系の物理学にはもう一つの側面がある。それが構造形成の物理であり、カオスやリズム現象などの複雑な運動形態を扱う非線形動力学である。両者は同じシステムが平衡状態から離れるにしたがって示す運動の異なった様式であり、その意味では同一線上でつながっている。我々の身の周りには、エネルギーが注ぎ込まれることによって初めて形作られ保たれる秩序構造が数多く存在する。私達の存在を含む生命そのものがエネルギーや物質の流入と排出がなくては成り立たないものである。生きているという状態を保つためには常にエネルギーの消費が必要であり、エネルギーの消費をやめた途端、生命という状態はただの物質の集まりである死に向かって急速に降下を始めてしまう。そのような存在が生命である。経済や社会も似たような側面を持っていると言えるかもしれない。生命や社会現象の複雑さには圧倒されるものがあるが、私達はそれ以前に自然現象にも至る所に同様の性質をもった現象があることに気づかされる。しかも我々が物理や化学で理解できると信じて疑わない自然現象でさえも非平衡状態に関しては驚くほど分かっていないことが多いのだ。注)
構造形成の物理あるいはパターン形成の物理は、非平衡状態で秩序構造がどのようにして形成されるかを扱う。この分野では例えば、渦巻く流れや湧き上がる雲、砂丘に立ち現れる風紋、雪の結晶の樹枝状構造といった、ひとりでに形が作られる現象についてそのメカニズムとそれらに共通する原理を探求することを目的としている。これらの構造はすべて系の外部とのエネルギーや物質のやりとりがあって作られる。熱の移動、風による運動量の注入、砂粒や水蒸気の流入、結晶化による潜熱の発生と拡散など、外部とのエネルギーの出入りがあるシステムを開放系と呼ぶが、ここであげた例はまさに非平衡開放系であり、私達が普段目にするものの多くは実は非平衡開放系であると言っても過言ではない。平衡系以外を全て非平衡開放系とひとくくりにして、これらのシステムを支配する法則はあるのだろうか、と問いかけるのは漠然としすぎているかもしれない。しかし物理学は、このように複雑な自然現象に対しても一種の理想化を行い、典型的な非平衡現象について徹底的に研究し尽くすことで、そこから普遍的なものを見出そうとする。物理が長年かけて培って成功をおさめてきた手法で非平衡系に挑めばよい。できるだけ単純な非平衡系で構造ができる現象に焦点をあてて、実験と理論のキャッチボールを繰り返すことで本質的な理解に迫っていくのだ。
流体の対流によって作られる周期的な渦の構造をレーリー・ベナール対流(あるいはベナール対流)と呼ぶが、この現象は80年代から非平衡開放系の典型例として、私自身を含めて多くの研究者によって研究されてきた。ここでは少し、ベナール対流を例に取り、自己組織化からカオスに至る道すじについて述べてみよう。ベナール対流系とは、平行な2枚の平板の間に流体を入れ、下から熱し、上から冷却して熱を流したときに、図6のように空間的に周期的な渦構造が現れる現象である。上の板を取り去って自由な表面で冷却すると表面張力の効果で蜂の巣状の六角柱の繰り返し構造が現れることも広く知られている。このような周期的な構造は、気象や地球物理、地質などで見られる周期構造を議論するときしばしば引き合いに出される。例えば、うろこ雲やいわし雲などの斑点状の周期構造や、マントルの対流、凍った湖が融け始めた際に観測される氷の6角形構造、玄武岩が冷却過程で割れてできたと考えられる柱状節理に見られる六角柱の繰り返し構造など、様々の現象で周期構造形成の原因にはベナール対流が関わっているとする説明が多く見られる。非平衡の物理では、これらの多様性にしばらく目をつむり、できるだけ単純で制御された実験でベナール対流を作り、上下の温度差を徐々に増加させていったらどうなるかをつぶさに観察し、定量測定を行うのである。図6は、横軸が温度差を表し、右に行くほど平衡状態から離れていくことに相当している。左端は、温度差がない状態で、平衡状態に相当する。温度差が増加したとき最初に現れる構造がロール状の渦の周期構造である。さらに温度差を増加させるとそのロールがうねり始め、時間的に振動を始める。この状態は、リミットサイクル振動と呼ばれる周期運動であり、非平衡状態で現れるリズム現象の典型例である。さらに温度差を上げるとロールの振動は徐々に複雑な振動となり、同じ振動の繰り返しではなくなる。数学的にはこの状態は、周期が無限に長く、わずかの初期値の違いが時間とともに指数関数的に拡大され、将来の状態が予測不可能になるため、カオス状態と呼ばれる。ベナール対流を始めとするカオスの研究により、現在では乱流の発生は力学系のカオス発生によるものと理解されるに至った。平衡からさらに離れた状態では、自由度の数が圧倒的に多いカオス状態が出現し、それが乱流状態であると解釈されている。カオスの発見は、ニュートン力学の成立から統計力学建設過程にいたるまで議論されてきた問題、すなわち決定論的な方程式が与えられたとき、初期条件を決めれば将来は完全に予測できるとするラプラスの悪魔の問題が量子力学のミクロな世界を持ち出すまでもなく、古典力学の範囲でも原理的に否定されたことを意味している。
重要なことは、平衡から離れるにしたがって空間構造や時間構造、カオスや乱流状態といった転移現象が次々と現れること、しかもこの次々と現れる転移現象は流体に限らず、化学反応やレーザーの発振現象、半導体中の電子・ホールプラズマ、粉体など殆どあらゆる非平衡開放系に共通して現れる性質であるという事実である。従来の物理学では各々の系は別々の方程式で記述されるのだが、非線形動力学の手法により、現象が起こる転移点に着目して重要な運動の自由度を切り出す、縮約という手法を用いることにより、異なった系が同じ方程式で記述できることが明らかになっている。それは構造形成の研究の大きな成果の一つでもある。
|
|
終わりに
今回の展示でも扱われた他の主題に相対論と量子論がある。物質の成り立ちを探求し、原子・分子から素粒子、クオーク、さらには4つの力の統一を目指す弦理論へと物質の階梯を下って根源をつきつめて来た物理学が、めぐりめぐって宇宙の創生とつながるストーリはいつ聞いても壮麗で美しいものである。しかし最初の方でも述べたように、その中心に位置する我々という存在やその思考や認識の基礎となっている身の周りの自然現象は素粒子が分かっても全て分かるものでは決してない。多数の要素が集まり、非平衡状態で出現する現象を理解するには、物質を理解するではなくその運動形態や集団的振る舞いを記述する言葉や数理が必要なのだ。 21世紀の科学には、生命現象や地球システムなどを含む、従来より格段に複雑な問題を扱うことも求められている。その中にあって、ものの記述だけではなく、ことの記述をも可能にする物理学の手法、そして分野を横断し、諸分野の知識を統合してゆくものの見方、考え方は、21世紀においてますますその重要性を増してくるのではないだろうか。 |
参考文献
ジャン・ペラン:「原子」、岩波文庫
米沢富美子:「ブラウン運動」、(共立出版)
寺田虎彦:「自然界の縞模様」、寺田虎彦随筆集(岩波書店)
寺田虎彦:「日常身辺の物理的諸問題」、寺田虎彦随筆集(岩波書店)
|

