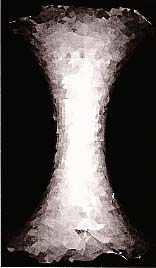
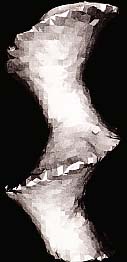
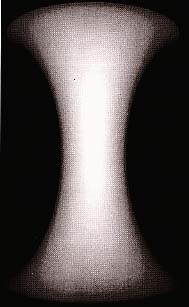
東京大学大学院数理科学研究科所蔵の幾何学模型
|
池水美都 文学部・美術史学 増田智仁 大学院情報理工学系研究室・コンピュータ科学 |
|
東京大学大学院数理科学研究科には、数式によって定義される曲面を三次元のモデルで表現した、ドイツ製の幾何学模型が200点あまり保管されており、現在その一部が数理科学研究科棟の資料室などに展示されている。あわせて所蔵されているドイツ語のカタログ[MARTIN SCHILLING 1904]から、模型の製作時期は19世紀末から20世紀初頭であったことが推測できるが、東京大学名誉教授の彌永昌吉先生によれば、これらの模型は、東京大学理学部数学教室に1904年から1937年まで在職された中川銓吉先生が、第一次世界大戦中あるいはそれ以前に輸入されたとのことである。当時は理学部数学教室の授業にも模型が用いられたようである[1]。 この模型のうち、おもなものはドイツのマルチン・シリング社の製作によるもので、石膏どりと呼ばれる、粘土のオリジナル模型から石膏で複製を製作する方法によってつくられている。そのため、現在では同じ模型が世界のいくつかの場所に存在しているが、数は非常に少ない。このような模型の、現在もっとも完全なコレクションが継承されているゲッティンゲン大学の資料によると、模型の組織的な製作が始まったのは1870年頃だとされる。1873年のベルリン科学アカデミーの月報に、アカデミーの会合で当時のドイツを代表する数学者の一人であるクンマー(E.Kummer)が、彼自身の製作によるシュタイナーのローマン曲面のモデルを披露し議論が行われていたことが記されている。また、マルチン・シリング社のカタログの解説中にはクライン(F.Klein)、ブリル(A.Brill)らの名前も見え、当時、一線で活躍した数学者が模型製作のプロジェクトに関わっていたことをうかがわせる[2]。 模型には、おおまかにわけて、代数曲面とその特異点の構造を扱った代数幾何学に関するもの、定曲率曲面、極小曲面などを扱った微分幾何学に関するもの、楕円関数など複素関数論に関するものに分けられる。これらの模型は、いわゆる概念模型ではなく、数値計算に基づく精密なものである。しかし、製作の技術的側面に関して残っている文献は一点のみであり[Catalog der Modellsammlung 1882]、このような正確な模型がどのようにしてつくられたのかについての詳しいことは不明とされてきた。模型の製作は、第一次世界大戦によって中断され、その後、模型の需要の減少などにより、それまで製作にあたってきたマルチン・シリング社は、1932年をもって製作を中止する。これは抽象代数学の基礎の確立と期を一にし、象徴的である。50年代以降、幾何学の研究も抽象化していくのだが、こうした流れの中でも、幾何学的対象を実際に「見る」ことは、理論的な側面と同様の重要性を常にもっており、模型の意義も失われなかった。視覚化することの重要性については、例えば、フラクタルの理論などは、20世紀初めにすでに理論の萌芽があったが、数学者がコンピュータ・グラフィックスの技術を用いることで実際に視覚化することができるようになってから、急速な発展を遂げていったことが挙げられる。幾何学的対象の実体を見たいという欲求は研究者には常にある。平面に投影した図の上だけでは、三次元の情報が視覚化困難であるが、その点、三次元の模型には実在感があり、あらゆる方向から視覚的に数学の問題を認識することが可能なのでその重要性は想像にたやすいだろう。こうした見る行為は、理論的な側面と一体となって数学の発展を支えているのである。 幾何学模型と20世紀美術東京大学数理学研が所蔵する模型コレクションの一部は、1997年に東京大学で行われた創立120周年記念「学問のアルケオロジー」展に出品され、安田講堂に展示された。その際には、数学者以外にも建築家や芸術家など、さまざまな分野からの注目を集めた。球面や放物面など比較的単純な曲面は身近なものであるが、例えば「いたるところ曲率が負の一定値をとる」といった高度な幾何学的要請から必然的に決定される曲面の「形態」としての魅力は、分野の枠を超えて、見るものに訴えかける。コンピュータ・グラフィックスにもまさる模型の圧倒的な量感と、式に導かれてできあがるこの必然の形態の魅力は、数学者のみならず多くの人たちを惹きつけたが、この幾何学模型の造形美は20世紀の芸術家たちを刺激し、創作活動にも影響を及ぼしている。 美術の歴史の中では、特に近代彫刻に対する幾何学模型の影響が指摘できる。東京大学と同じ幾何学模型が、パリのアンリ・ポワンカレ研究所にあったが、それを「発見」したのはマックス・エルンストである。模型について『カイエ・ダール』誌のディレクター、クリスチャン・ゼルボスに話したところ、ゼルボスがマン・レイに写真をとるように依頼したという[3]。マン・レイは何十もの模型の中からいくつかを選んで撮影し、うち12枚が1936年の『カイエ・ダール』誌に掲載された[4]。このマン・レイによる「数学的オブジェ」の写真や幾何学模型そのものは、さまざまな展覧会で展示され、亡命先のハリウッドでは、1948年には、写真に基づいて絵画作品も制作されている[5]。 マン・レイはおもに石膏による幾何学模型を好み、そこから影響を受けていたが、その一方で、イギリスの彫刻家ヘンリー・ムーアは、1937年から39年にかけて、弦を用いた模型に関心をもち、作品を手がけている。これは、ムーアがロンドンの科学博物館で見た弦による数理学モデルに影響を受けてつくったという。ここでムーアが魅了されたのは、模型の形態や量感よりもむしろ中が透けて見えるという性質だったようである。西欧における構成主義的彫刻の中心的人物となったナウム・ガボもそうした幾何学模型からの影響を受け、幾何学的な形態を多用し、水平・垂直を強調した作品を制作している。そしてガボの兄であるアントワーヌ・ぺヴスナーも、模型からの影響を否定しているとはいえ、類似の形態を用いている。ムーアは1939年以降、弦を用いた作品を制作しなくなるが、バーバラ・へップワースが1939年から「木と紐」のシリーズで弦を用い始め、ムーアの方法を引き継いでいく。また、ムーアの弟子であったアンソニー・カロも二重化、三重化された面が透けて重なり合って見えることへの関心を引き継ぎ、それを発展させていく。シュルレアリストによって注目され、雑誌に掲載されたり展覧会に展示された幾何学模型は、芸術家たちを介し、それぞれの異なった解釈によって、本来の数理模型の意図した目的とは離れた部分ではあるが、20世紀の彫刻に影響を与えることになったのである。 レンジセンサーを用いた幾何学模型の形状評価幾何学模型は概念模型ではなく、数値計算に基づいた精巧なものである。今回はこの1世紀前につくられた模型がどれくらいの精度でつくられていたのかを解き明かすため、生産研究所池内研究室のもつレンジセンサーの技術を用いて調査を試みた。
1 数理模型の三次元形状測定とモデル構築数理模型の形状評価をするためには、まず最初に現存モデルの三次元形状を測定しなければならない。ここでは、レーザーレンジセンサーを使うことにより、模型をあらゆる方向からできる限りオクルージョンをなくすようにレーザースキャンして、複数の距離画像(レンジデータ)を得、その後、それらの距離画像をアラインメント[6]、マージング[7]という作業を通して物体形状データを三次元表面点列として得た。以下では、レーザースキャン、アラインメント、マージングの技術についての概略を示す。 1.1 レーザースキャン今回測定した模型は、幅、奥行き、高さとも0.5メートル以下のものだったため、0.8メートルから1メートルレンジを計測できるPulstecのTDS1500を使用した。このレンジセンサーは、発光窓から発射されるレーザーを受光窓で捕らえたときの視差によってレンジを測定する、三角測量法に基づいて設計されている。このスキャンにより、三次元表面点列データが得られる[図1、2]。
1.2 アラインメント得られた距離画像から模型に無関係な点列データを削除した後、それぞれの距離画像を1つの座標系上に適切に配置しなければならない。ここでは、手動で距離画像間の初期位置を合わせ、その後自動的に逐一画像間の対応点を計算し、一致させるプログラムを使うことによって位置合わせ(アラインメント)を行った。さらに、対応点の存在する2つの距離画像を個別に合わせるだけでは、全体的な形状の対応に誤差が生じるため、最後に同時位置合わせ(サイマルテイニアス・アラインメント)を行った。1.3 マージング距離画像をアラインメントしただけでは、ただ単に複数の距離画像が重なって置かれているだけなので、これを1つの形状にまとめあげなければならない(マージング)。本計測においては、コンセンサス・マージングという手法を用いた。対応している複数の距離画像の面の境界でコンセンサスを取り、どのように点を置き、面(ポリゴン)を貼るかを決める手法である。これらの計算にはかなりの資源が必要なので、Pentium 1GHz・メモリ1GBのPCを8個つなげたPCクラスタを使い、計算の並列化を図った。こうして現存モデルを構築した[図3、4、5、6]。
2 数理模型からの理想曲面のパラメタ推定2.1 各々の模型に対応する理想曲面
2.2 初期位置合わせ理想曲面との差異を調べるためには、計測形状を三次元座標軸上に適切に配置しなければならない。本計測では、まず大雑把なパラメタ調整によって、計測形状に近い理想曲面の形状を得、理想曲面をベースにした計測形状のアラインメントを行うことによって、三次元座標軸上に適切に配置した。2.3 関数フィッティング計測形状の初期位置合わせで用いた理想曲面を初期解として、各パラメタを範囲を決めて全探索し、計測された表面点列と理想曲面の点列との対応点を求め、その距離を最小にするパラメタを求めることにした。対応点計算においては、計算量を少なくするためにkd-treeviiiを用いた探索を行った。以下は、各関数において推定して得られたパラメタである。
3 数理模型と推定された理想曲面との比較本計測ではさらに、以上で得られた推定パラメタから求められる理想曲面と計測形状との間に、どれだけの差異があるかを調べた。理想曲面と計測形状との対応点を計算し、その距離がどの程度であるかを調べた結果を以下に図で示す[図11、12、13、14]。
4 まとめ本計測では、レーザーレンジセンサーによって得られた三次元表面点列を、アラインメント、マージング等の処理を通して既存の数理模型の形状モデルを構築した。そのモデルからパラメタを推定し、さらに推定されたパラメタを適用して得られる理想曲面と、形状モデルの差異を求めた。 計測機の精度が原因で生じる測定誤差や、数理模型自体が経年変化を遂げて石膏が欠けてきているような点などを考慮にしても、数理模型の精度はかなりのものであることがわかる。多少の誤差があるという結果は出たが、数理学的な問題を実感として捉えていく上では、とても貴重なものであることに変わりはない。そしてこうした数理模型は教育目的で使う上では、充分な精度をもっていたといえるだろう。今回は比較的測定しやすい模型を選んで形状評価をしたが、さらに複雑な形状をしている模型についても調査を行うと興味深い結果が出るかもしれない。 最先端技術レンジセンサーを使った三次元スキャニングによって文化財は立体的に記録されるだけでなはなく、得られたデータは今後、保存、修復、研究、鑑賞等に役立てていくことができる。貴重な歴史的文化遺産は、日々、風雨による劣化や不測の事態による破損、焼失などの危険にさらされているが、こうした文化遺産の三次元デジタル化が進めば、今後は実物を一切傷つけることなく、さまざまな切り口での解析や修復作業のシミュレーションを行うことが可能になる。そして将来的にはこうしたアーカイブ化の技術を応用して、日本の文化財についての歴史、幾何情報、光学情報、環境情報などを統合させてコンテンツ化し、サイバー空間へ永久保存することが現在目指されているという。
|