第2部 展示解説/鉱物界
REGNUM LAPIDEUM
鉱物界の進化
鉱物の形の多様性
鉱物は約4000種が知られているが、多くの鉱物はそれぞれ特有の形と色を示す。ここでは鉱物の形の多様性を考えてみよう。異なった鉱物種が同じ形態を示すこともある一方、一つの鉱物種が複数の形態を示すこともある。例えば、黄鉄鉱(FeSz)には直方体、正八面体、三角十二面体などの形が観察されるし、ダイアモンド、黄鉄鉱、スピネルはともに正八面体を示す。またジルコンも八面体を示すが、正八面体 ではなく、少し上下が潰れている。多くの鉱物が示す形態を調べてみると、そこにはある法則性があることがわかる。例えば、直方体と正八面体を比べてみると、そこに共通点がある。比べるのは「対称性」 である。
「対称性」ある図形を(かたちを変えることなく)移動した時、移動後の図形と移動前の図形が重なる (即ち移動したか否かがわからない)場合、その図形は対称的であるといい、対称となるようにする操作を 対称の操作戒いは対称要素という。
直方体の例でいうと、対称操作は直方体をある軸のまわりに回転することである。直方体の正方形の相 対する面の中心を軸として90度回転すると、回転前と同じ位置にくる。360度回転する間に4回同じことが起こる(4回回転対称があるという)。また、直方体の体対角線で見てみると、120度回転すると回転前と同じ位置に来て、360度回転する間に3回同じことが起こる(3回回転対称がある)。また、相対する稜の中点でみると、180度回転すると回転前と同じ位置にきて、360度回転する聞に2回同じことが起こる (2回回転対称がある)。
正八面体では、相対する頂点を軸として90度回転すると、回転前と同じ位置にくることから、4回回転対称があることがわかる。相対する正三角形の中心を結ぶ軸でみると、120度回転すると回転前と同じ位置にくることから3回回転対称がある。また、相対する稜の中点でみると、180度回転すると回転前と同じ位置にくることから2回回転対称がある。そして4回回転対称と3回回転対称と2回回転対称の相互の位置関係が同じである。即ち、対称性という点では正八面体と直方体は同じになる(図1)。
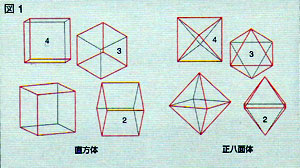
[ 鉱物の対称性 ]
では、このような対称性が鉱物のどのような性質からもたらされるのであろうか。
鉱物は天然に産する一定の化学組成をもつ固体の無機物質である。鉱物の結晶は、鉱物を構成する元素 の原子が化学組成に示した割合で互に結合し規則正しく配列した構造をもっていることによって特徴 づけられる。互に結合した原子の規則正しい配列によって構成されている結晶は、基本構造単位の周期 的な配列と考えることもできる。その基本構造単位は単位胞と呼ばれ、結晶は単位胞の周期的な三次元 配列で成り立っているということができる(図2)。

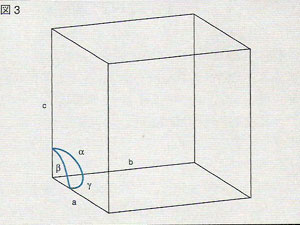
この単位胞の大きさと形を、単位胞の各辺に平行で互に交わる3つの軸を考え、その長さと軸間の角度で記述する(図3)これを格子定数という。
鉱物を構成している原子は、結晶の中で無秩序に配列しているのではなく、その原子特有の結合の仕方に従って他の原子と結合している。例えば、ケイ酸塩鉱物の中ではSi原子は、酸素と結合するときに、正四面体的な結合をする。即ち、Siは正四面体の中心に位置し、Oは正四面体の頂点を占める。また、Mg は頂点にOを配置した正人面体の中心に位置する(図4)。
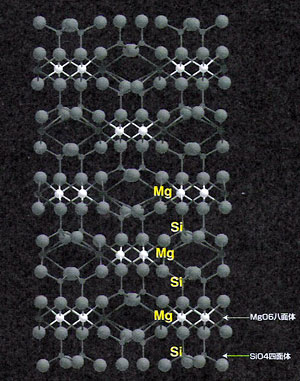
もちろん、実際の結晶においては、厳密な正四面体や正八面体ではない。このような、原子特有の結合の仕方は、多かれ少なかれすべての原子について存在する。これは原子の周りの電子分布の特徴に依存 し、他の原子との結合の仕方にも依存する。その結果、結晶中の原子の配列には、ある程度の規則性が生れ、そこに対称性が生じるようになる。