第2部 展示解説/鉱物界
REGNUM LAPIDEUM
鉱物界の進化
鉱物の形の多様性
結晶の対称性には大きく分けて2種類ある。即ち、結晶の形態や光学・電気伝導度・圧縮率など物理的 性質の示す対称性と結晶を構成している原子の配列の示す対称性である。一方はマクロ(巨視的)な性質の対称性で、我々が直接に測定可能だが、他はミクロ(微視的)な性質の対称性で、原子の配列の対称性 である。両者は、もちろん無関係ではなく、結晶を原子のオーダーで見るか、目で見える大きさで見るかの差である。 X 線が発見され、それが結晶の中の原子の配列を決定する最初の実験的手段を与える までは、もっぱらマクロな性質の対称性が研究の対象であった。特に、鉱物学では結晶の示す形態の対称性が主要な研究対象であった。
結晶の形態を研究する手法は、結晶に現れる面の間の角度を測定することであった。18世紀の中頃までには、多くの鉱物について、その面間の角度の測定が行われ、その中から「面角一定の法則」 、 「有理指数の法則」が経験的に確立された。「面角一定の法則」は、同一の結晶が様々な形態の様相 を示しても対応する結晶面の間の角度は一定である、とするものであり、「有理指数の法則」は、結晶に現れる面を記述するための指数(Millerの指数)は有理数である、とするものである。
物質を大別すると、結晶と非結晶に分けることができるであろう。結晶にあって非結晶にない巨視的な性質のもつ特徴として、均質性と異方性がある。先に述べた巨視的な性質とは、形態、光学・電気・磁気・熱的性質などの測定ができる物性のことをいう。均質性とは、結晶のどの場所でも、ある一定方向の物性は同じであることであり、異方性とは、結晶の一点において、物性が方向によって異なるこ とをいう。非結晶は理想的な場合においては均質性を実現できるであろうが、異方性を実現することはできない。この均質性と異方性という特徴は、結晶を作りあげている原子が規則的な配列をしていることから導かれるものであり、結晶構造は、構成している原子が、単位胞を基本として3次元的に規則正しく周期的配列したものとして理解することができる。単位胞が3次元的に規則正しく周期的配列していることは、巨視的な観点からみると結晶のどこの点(マクロなサイズにおいて)でも、同価であることを意味しており、従って、結晶の均質性が導かれる。一方、単位胞内での原子の配列は一般的に異方的である。この異方的な単位胞が3次元的に規則正しく周期的配列していることは、巨視 的にも異方性が保持されることを導く。従って、異方的な原子配列を基本とする結晶は、本質的に均質であり異方的である。
結晶が単位胞の3次元的周期配列で成り立っていると考え、単位胞を1点で代表する。その点の集合は、 結晶構造から単位胞の周期配列のみを抽出したものといえる。この点の集合を格子(一般的に3次元で あるために空間格子と呼ぶ)、個々の点を格子点と呼ぶ(図5)。

結晶における格子点の配列は結晶格子とも呼ばれる。結晶格子をその基本単位となる平行六面体・単位格子:unit cell- で代表させ、単位格子の3つの互に平行でない3稜の長さ a,b,c と互になす角度α,β,γで単位格子を記載する(格子定数)(図3)。一般的に格子の選択の仕方は無限である。しかし、後述する格子点の配列の対称性を考慮して、最小の単位格子を決めることが原則である。結晶構造で定義した単位胞と結晶格子で定義した単位胞は同一であるものとする。
[ 結晶面 ]
結晶の外形に現れた面を結晶面というが、この結晶面は結晶格子で定義される結晶画に平行である。 結晶格子の格子定数を a,b,c とすると、ある格子面が結晶格子の a軸, b軸, c軸とma,nb,pcで、交わったとき、その結晶面の指数を1/m, 1/n, 1/p とし、これを整数化して面の指数(hkl)とする。例えば、ある結晶面が a軸, b軸, c軸とそれぞれ 2a,3b,4c で、交わったとすると、面の指数は 1/2,1/3,1/4 で、これを整数化して(643)がこの結晶面の指数である。
[ 結晶格子の対称性 ]
先ず、結晶格子には格子の平行移動という対称操作が存在する。即ち、単位格子をその格子の整数倍だけ平行移動しても、移動後の図形と移動前の図形が重なるため、格子並進という対称操作が存在することがわかる。
次に、格子の並進以外にどの様な対称操作が可能であるか考えてみる。並進の要素を含まない対称操作について、即ち結晶格子を固定して、結晶格子の対称を考える。この場合、対称操作として可能なものは、回転対称、回反対称である。回転対称とは、原点の周りに 2π/N回転した時に、移動後の図形と移動前の図形が重なる対称操作である。結晶格子が単位格子の周期配列であるとの制約で、 N は1,2,3,4,6 に限られる(定永,1986)。
回反対称は回転操作に引き続き中心対称の操作を行う。回反対称は回転対称と同様に 1,2,3,4,6 回回反対称 (

図6はステレオ投影法と呼ばれる方法で描かれている。この投影法を説明する(図7)。ステレオ投影法は、 3次元空間における方向を2次元に投影する方法の一つである。原点Oを中心にした球を考える。 結晶面Pを投影する場合、原点を通ってその面に垂直な線 r が球と交わる点を A とする。 A が球の北半球部にあるときは、Aと南極を結び、赤道面との交点Bで結晶面を代表させる。また結晶面 が南半球にあるときは、南極とCとを結んだ線と赤道面の交点Dは球の外に出るために、この場合は、 北極と結び、赤道面との交点Eで結晶面を代表させるが、結晶面が南半球にあることを表すために交点 の記号を変える。この投影法をステレオ投影法と呼んでいる。

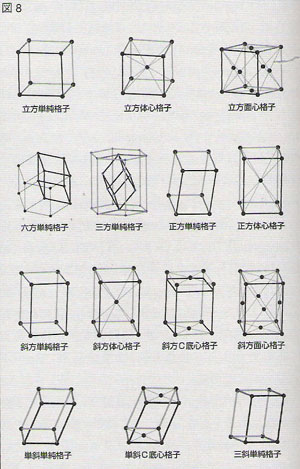
結晶格子には何種類が可能か、という問題に対して格子の積み重なり方と格子の対称性から14種の格子を導き出した。14のBravais格子である(図8)。