第2部 展示解説/鉱物界
REGNUM LAPIDEUM
鉱物界の進化
鉱物の形の多様性
[ 結晶系 ]
14の格子をその対称性で分類する。「対称性で分類する」とは、格子がどの様な対称要素をどの様な配置 でもっているかで分類することである。回転及び回反対称に基づいて分類する。格子は本質的に中心対称 をもっていることに注意する必要がある。 格子が1回回転対称(+ 中心対称)のみをもっ場合、三斜晶系 (triclinic) といい、格子定数は a≠b≠c, α≠β≠γである。格子が2回回転対称(+中心対称)のみを 有する場合は、2種類ある。一つは、2回回転対称が1方向のみに存在する場合で、単斜晶系 (monoclinic) といい、a≠b≠c,α=β=90°γ≠90°である。他の一つは、2回回転対称が3方向に存在する場合 である(2方向のみに存在することはあり得ない)。この場合は斜方晶系(orthorhombic) で、a≠b≠c,α=β=γ=90° である。格子が3回回転対称を有する場合は、3回回転軸は格子の体対角方向にある。この場合は三方晶 系(trigonal)で、 a=b=c, α=β=γ≠90°となる。格子が4回回転対称を有する場合は、 4回回転軸 はc軸方向に存在し、正方晶系(tetragonal) で、 a=b≠c, α=β=γ=90°である。また、格子が 6回回転対称を有する場合は、6回回転軸はc軸方向に存在し、六方晶系(hexagonal)でa=b≠c, α=β=γ=90°となる。最後に、2回あるいは4回回転対称が a,b.c軸の3方向に存在し、更に3回回 転軸が体対角方向にある場合、立方晶系(古くは等軸晶系)で、a=b=c, α=β=γ=90°である。
この分類法で格子を分類すると、三斜晶系・単斜晶系・斜方晶系・正方晶系・三方晶系・六方晶系・立方晶系の 7つの結晶系が得られる。
[ 点群 ]
光学的性質、電気伝導度、圧縮率などの結晶におけるマクロな物理的性質の対称性を考える。 これらの物性は一般的に異方的であり、そのために結晶の中の1点を代表点として選択し、その点に関する物性の対称性を論ずれば良い。例えば、その物性がベクトルで表される場合を考えると、原点に一端を置くベクトルの空間分布の対称性は、並進を含まない対称要素の原点における組み合わせを考え ることである。この対称要素の組み合わせは群をなし、32種類存在する。これを32の点群という(図9) 。
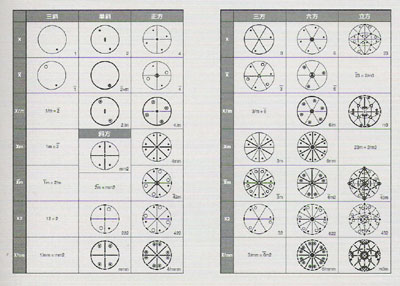
図9 32の点群(対象要素と同化点の分布
32点群の導き方は7結晶系の導き方と基本的には同様であり、図の左の項に示された X 、
三斜晶系には、上に述べたようにXとしては1のみ可能であり、X/m以降は存在せず、点群としては1、
単斜晶系は上に述べたように b 軸方向にのみ対称が存在し、対称要素は 2 と
Xm 以下は対称要素が b 軸以外に存在することから対称は斜方晶系になる。斜方晶系では記号の順番は a 軸、b 軸、 c 軸の順番である(表参照)。可能な対称要素の組み合わせは各軸方向の
2 と m の組み合わせで得られる。 即ち、2m(Xm)、
正方晶系はc軸方向に4回回転軸を持つことが特徴であり、このことから a 軸と b 軸は同価となり、 新たに対角方向に対称要素が生じる。従って、記号の順番は表に示す様に、C
軸、a 軸、対角方向 [110] となる。図の X が 4 であり、 4 と m または 2 との組み合わせによって、正方晶系として 4,
三方晶系は、やや複雑であり、先ず六方晶系を説明する。六方晶系は c 軸方向に六回回転軸を持つこ とが特徴で、正方晶系同様に a 軸と b
軸は同価となり、新たに対角方向に対称要素が生じる。 従って、記号の順番は表に示す様に、c軸、a軸、対角方向 [210] となる。図の X が
6 であり、 6 と mまたは 2 との組み合わせによって、六方晶系として 6,
前項で、「格子が 3 回回転対称を有する場合は、 3 回回転軸は体対角方向にあり、三方晶系 (trigonal) で、 a=b=c, α=β=γ≠90°と記したが、この格子の取り方が直感的に理解しにくいために、
一般的には、3回回転軸を C 軸にとって、六方晶系と同じ軸の取り方で記述する。但し、対角方向の 対称は生じない。 X を 3 として 3 と
m または 2 との組み合わせから 3,
立方晶系の特徴は a 軸、b 軸、c 軸が同価で、あり、そのために体対角方向に 3回回転対称が生じる ことである。従って、記号の順番は表に示す様に、c
軸、体対角方向 [111] 、対角方向 [110] となる。 X としては 2、4を考える。その結果、生じる組み合わせは、23,
[ 空間群 ]
本項では、鉱物結晶の形態について考察するので、ミクロな結晶構造の対称性を記述する空間群については言及しない。詳しくは International Tables for Crystallography を参照。
[ 結晶の形態 ]
結晶の形態の対称性は点群によって与えられる。実際に出現する結晶の形態は、点群と現れる面の 組み合わせで決まる。
例えば立方晶系の点群 m3mを考える。面(100)が出現すると形態は図 10-2 のような立方体になる。 (111)、(112)、 (122)は、それぞれ図
10-2,3,4 のような形態を示す。また、面(123)は、立方 23,m3,
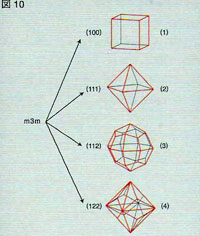 図10 点群m3mにおけるいろいろな面に対応する形態 |
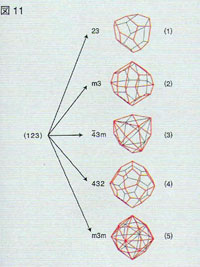 図11 面(123)が与えられたとき立方晶系の点群で見られる形態 |
このように、同じ点群でも出現する面が異なれほ重なった形態を示すし、異なった点群が異なった 形態を示すことも同じ形態を示すこともある。何故、ある鉱物が特徴ある形態を示すか、という ことについては実はまだ、よくわかっていない。はっきりしていることは、鉱物はそれぞれ特徴的な 結晶構造を持っており、その結晶構造の対称性(空間群)は点群に対応している。従って鉱物の示す 形態の対称性はその鉱物固有の形態である。ただし、上で見たように、同じ対称性でも異なった面 が出現して異なった形態を示す(同じ対称性でも)ことがしばしばみられる。例として黄鉄鉱 (FeSz) 、点群 m3の形態の多様性を図 12 に示す (Sunagawa,1957) 。
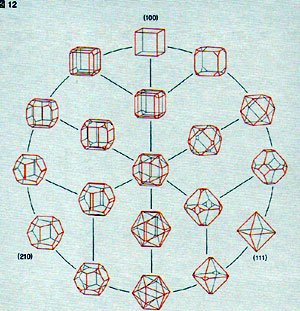
図12 黄鉄鉱に出現する多様な形態
出現する面は 3 種類で (100)、 (111)、(210)である。図に示されているのは、それぞれの単形とそれらの集形である。 この多様性は、黄鉄鉱の成長時の物理的・化学的条件の差によるとされるが、どのような物理的・化学 的条件のもとでどのような形態が出現するかは、ほとんど解明されていないのが現状である。