39 自然界は「自己複製」(コピー)を繰り返す——鉱物結晶の問題
|
結晶模型は鉱物学の講義で結晶の対称性や分類を学ぶために用いられるものである。コンピュータ・グラフィックスがまだ存在していなかった時代、結晶の立体構造を学習するには、立体模型を用いるのがもっとも効果的だった。平面図画から三次元構造を想像するよりも、実際に手にとってみて、その感触と視覚をクロスオーバーさせて認識した方が理解し易い。その点、結晶模型は最新のヴァーチャル・リアリティに勝るとも劣らない教育能力を備えている。 39-1 鉱物結晶モデル一式(約二百十点) 木製、ドイツ製、東京大学総合研究博物館鉱物部門 現在総合研究博物館の所有になる木製結晶模型は三種類に大別され、数にして700点を超えている。三種類のうち一つは近年まで理学部鉱物学教室で使用されていたもので、標本カードの存在は確認されていない。残りの二種は工学部の地球システム工学科の旧蔵品である。一つは抽斗が七つある小型の木箱に納められており、他の二種よりも一回り小さく、長軸が最大でも3センチに満たない。抽斗のうちの二段は、結晶の生成過程、結晶の形態分類など、テーマごとに整理がなされている。残りの五段には各鉱物ごとに可能な形のヴァリエーションが揃えてある。模型の表面には鉱物名が印字してあり、同一の鉱物について形の異なる模型が何種類かある。最後の一つはコレクションの原型を復元し難い状態にある。サイズは平均4センチ前後で、表面に標本番号が赤色で印刻されている。また各標本は木製小箱に入っており、標本カードを伴っている。標本カードについては後ほど詳しく述べる。番号整理の段階で、1番から60番までの模型は二種類あることがわかった。そして番号の重複する二つの標本は必ずしも一致しない。標本は総数210個あったと言われることから、1番から60番までと、1番から150番までの二系統が混在していたことになる。この標本セットの現在数は197個であり、23点が失われている。また、標本箱ないし標本カードの無いものも7点ある。1番から60番まで重複があるとすれば、33番、37番、57番、58番の計4点は本体も箱も紛失していることになる。逆に番号の書かれていない標本とカードが二組あった。 それぞれの模型の収められた小箱には二枚の標本カードが重なって入っている。カードは黄ばんで、さらに塵で黒く汚れているが、標本番号・結晶名・結晶の面を示す座標(面指数)およびその結晶構造をとる鉱物の具体例(黄鉄鉱など)を読み取ることができる。上の一葉には、最上段に「東京帝国大学工学部鉱物学科」(Department of Min. Eng. Tokyo Imperial University)と印刷してある。中段左には標本番号が付され、中央に結晶の和名、その下に英名がそれぞれ記入されている。下段には結晶の面指数が書かれる。右には、この標本で表された結晶のかたちをとる鉱物の実例が記載されている。この標本カードは、田賀井篤平教授によると、戦前理学部に出入りしていた鉱物愛好家桜井氏の手になるという。下の一葉の特徴は、美しい飾り罫と (近藤康久)
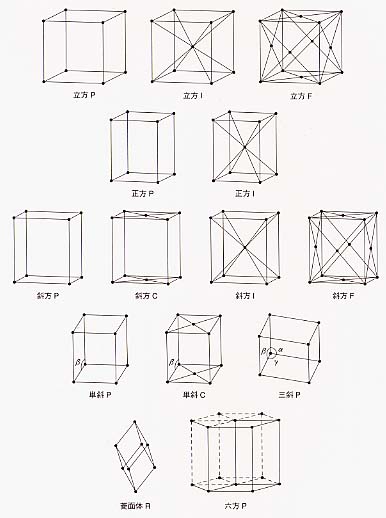
39-2 鉱物結晶モデル一式 木製、木製キャビネット入り、縦30.5、横43.5、高24.7、英国製、1875年7月、東京大学総合研究博物館鉱物部門 規則正しい形をした鉱物結晶は、古くから人々の眼にとまり、貴石として珍重され、さまざまな「能力」を付与されたりしてきた。たとえば、ダミゲロンやプリニウスが言及しているワシ石(aetites,eaglestone)は、内部が中空の一種のノジュールであるが、出産を促す能力があると考えられていた。だがなぜそれぞれの鉱物が独特の形や光沢、色を持って出現するのかを、充分に納得がいくまで説明することは、大きな困難をともなうことである。形に関してだけ見ても、規則正しさの再現性は同じ鉱物でも違っているし、種類が違えば形自体が異なってくる。一方で、いろいろなかたちで規則性の乱れが混入しており、表面の突出やくぼみ、包有物、さらには鉱物同士の相互に入り組んだ関係が現れる。無機物界における物体の発生と成長の問題の複雑性は驚くばかりである。 なるほど、原子論の復活していた17世紀西欧においては、たとえばロバート・フック(1635−1703)が『ミクログラフィア』において示したように、ビー玉状の粒子の寄せ集めで結晶のさまざまな形ができるという考えが成立していた。しかし同じ球状粒子が、なぜあるときは六角柱状の水晶となり、あるときは立方体の黄鉄鉱となるのか、と問われれば、当然そこに、基本粒子の形態の問題や構成原理の違いといった問題が生じてくる。植物がそれぞれの種類を種子というかたちを通して維持していくのと同様に、鉱物のさまざまな種類もそれと似た地中の幾何学的造形作用によって作られるという生気論的な考えが残っていったのも理解できるのである。 その後アユイ(1743−1822)による本原型の考えが提出され、演繹的に有利指数の法則を導出した。彼はたとえば方解石の「分子」は劈開片と同じく菱面体形であるとして、分離型分子(molecules soustractives)と不可分分子(molecules integrantes)から結晶構造の規則性が組み立てられると考えた。19世紀にはいると、数学的に洗練されたかたちで結晶形態学が完成されていくことになる。ヘッセル(1796−1872)、ブラヴェ(1811−1863)、ゾーンケ(1842−1897)らによる晶族や空間群の研究を経て、1890年から1895年にかけて230の空間群が、シェーンフリース(1853−1928)、ヒョードロフ(1853−1919)、バーロー(1845−1934)によってそれぞれ独立して完成された。 20世紀はエックス線による結晶構造研究で幕を開ける。ラウエやブラッグ父子らによってエックス線結晶学が形成され、寺田寅彦ら日本の科学者たちも足跡を残している。1930年代ころから結晶成長学に関心が集まり始め、単結晶に関する知見を必要とする半導体産業の成長とともに発展する。人工結晶についての研究が進み、1950年代にはダイヤモンドの結晶作製に成功した。今日ではコンピュータによる成長様式の再現が行われている。 工学部地球システム工学科旧蔵のセットは、英国王室のお抱え鉱物学者ジェームズ・テナントが1875年に製作したもので、凝った造りの木製キャビネットに収められている。この標本はその職人的な技術の高さからして一種の工芸品でもあり、芸術と科学が近接していた時代の博物学のあり方を今日に伝えるものと言える。 (山田俊弘) 39-3 水晶 木製台座付、採掘地不明、縦20.5、横31.5、高43.0、東京大学総合研究博物館鉱物部門 水晶の細部にわたる観察とその分析については、フックと同時代のステノのものが興味深い。彼は、最初の小さな種結晶がなぜできるのかについては知らなかったが、植物のような成長を否定し、いったん最初の結晶ができた後で起こる成長は存在する外部表面の上に流体から分離した粒子が付加することで起こるとして、結晶の様々な形態の変化を説明した。ステノはその『プロドロムス(固体論)』(1669年)において、固体を取りまく流体に二種類の運動を区別して結晶の成長を理解しようとしている。すなわち、ある一定の場所に結晶質物質が付加されるようになる運動と、それが面に広げられる運動である。これによって彼は結晶成長の異方性や晶相変化を巧みに解説し、図示している。それぞれの結晶が持つ面角の安定性という重要な規則性についての指摘はこうした文脈においてなされた。ステノの議論は、水晶にとどまらず、赤鉄鉱、ダイヤモンド、黄鉄鉱に及んでいる。 (山田俊弘) 絵画、彫刻、文学、そして教育教材としてのレプリカ、更にデジタル技術など、「コピー」は様々な分野で行われている。しかし、「コピー」はこのような、いわば人間の理性や意志に関する領域でのみ行われているものではない。例えば、自然界のあらゆる生物は遺伝子や細胞を「コピー」することにより存続している。そしてまた、理性や意志などといったものからは最も縁遠いと思われる無生物の世界にも、「コピー」現象は存在するのである。このようなものとして、本稿では鉱物結晶を取り上げる。 結晶とは物質のうち原子の規則正しく、周期的な配列から成り立っているもののことである(これに対し、結晶のように周期的な配列を持たない物質を非晶質、あるいはガラスという)。原子配列が規則的にコピーされることによって、結晶は規則正しい平面からなる形態をとる。 結晶の持つ規則正しい形は古来から驚愕の的となってきた。例として、正多面体に関して言えば、何種類の正多面体が存在するかという問題は、古代ギリシアにおいて解明されたことが知られている。正多面体として可能な立体は、正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類であり、俗にプラトンの多面体とも呼ばれている。自然界にはそのすべての形の結晶が存在し、幾何学が誕生するよりずっと以前から生成され続けてきたのである。 正四面体の結晶を持つ鉱物は比較的数が少なく、四面銅鉱(Tetrahedrite、アンチモン、或いは砒素を主成分とする銅鉱石の一種)の他には、閃亜鉛鉱(Sphalerite、ただし四面体を成すことは稀)や、比較的珍しい鉱石であるズニ石(Zunyite)、ヘルビン(Helvin)などが知られている程度である。が、その他の多面体の外形をした結晶を成す鉱物は多く、例えば黄鉄鉱(Pyrite)の結晶形には正六面体、正八面体、正十二面体、正二十面体の4つの多面体のすべてがある。この他、正多面体ではないが、二十四面体、四十八面体など、かなり複雑な形状の結晶がある。 結晶はこのように規則正しい形態を形成する一方、また、鉱物の種類に応じて多様な形を持つ。では、結晶とは具体的にどのような構造を持っているのであろうか。以下に、結晶の外形が持つ規則性と、結晶の内部構造、そして両者の関連について述べてみよう。 鉱物学では、結晶を、結晶が持つ対称性によって分類している。対称性の要素には回転軸、対称面、対称心、回反軸の4つがある。 第一に、回転軸とは、立体を、その軸を中心に回転すると、一回転する間に何度か同じ空間を占める位置があるというものである。例えば、正六角柱の場合、長軸の周りに60度回転すると元と同じ形態になり、これを六回繰り返すと一回転して元の状態に戻る。この場合を六回回転軸がある、という。一般に回転軸は二回、三回、四回、六回のものがある。 第二に、対称面とは、鏡面ともいい、面に関して対称になるということで、鏡に映す場合と同じ関係である。 第三の対称心は、反転ともいう。ある図形が、一つの点を中心に点対称となる場合、その点を対称心といい、その図形には対称心がある、という。 第四に、回反軸とは、ある角度回転し、更に反転すると同じ形態になる、という対称要素である。同じ操作をn回繰り返すと元の状態になる場合をn回回反軸を持つ、という。一、二、三、四、六回の回反軸が考えられる。が、一回回反軸を持つということは対称心を持つことと同じであり、二回回反軸は対称面を持つことと同じで、三回回反軸は三回回転軸を持ち、かつ対称心を持つことと同じ、そして六回回反軸は三回回転軸を持ち、かつ対称面を持つことと同じである。したがって、四回回反軸だけが他の三つとは独立した対称要素である。結晶でどのような対称要素が組み合わせられるかを調べると、その組み合わせは三十二通りあり、これを三十二晶族という。 三十二晶族は、結晶の単位格子又は形態の対称性により、7つに分類される。結晶は、構成原子が規則正しく配列しているので、その原子配列の最小単位を包含する平行六面体を考えることができる。このような平行六面体を単位格子という(結晶を、単位格子が三次元的に積み重なったものと見なすのである)。今、この単位格子の頂点のうち一つを選び、そこから伸びる三本の辺をa、b、cと名付ける。また、b、cの成す角をα、c、aのなす角をβ、a、bのなす角をγとする。すると、これらの辺の長さ、及び其々の角度により、結晶は7通りに分類されることになる。これを七晶系という。 さて、ここで更に、結晶の原子配列についてみてみると、単位格子である平行六面体の各頂点のみに原子がある場合の他に、格子の中心にも原子がある場合、相対する面の中心にも原子がある場合、6つの面すべてに原子がある場合がある。したがって、原子の配置と単位格子の形(すなわち晶系)と組み合わせて考えると、単位格子には14の型があることになる。重複があるので単純に七の四倍とはならない。これは発見者の名にちなんでブラヴェ格子と呼ばれている[図1]。
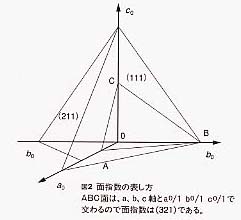
以上のように、結晶は多様な外形を見せるとはいえ、その根元にある内部構造は、僅か7通りの晶系に分類でき、原子配列にしてもたった14通りの型に分類される単位格子の単純な繰り返しに過ぎないのである。 結晶の外に現れる平面は原子が配列した面(原子網面)である。こうした結晶面を区別するためには面指数(ミラー指数)が用いられる。それは次のようにして得られる。先程、単位格子に対して設定したa、b、cを、基準とした頂点を原点とし、各辺の方向に伸びる3本の座標軸としよう。各辺の長さはa0、b0、c0とする。ある結晶面ABCが座標軸を(1/h)a0:(1/k)b0:(1/l)c0、で切る場合、この面の面指数は(hkl)であるという[図2]。後出の結晶模型標本で、模型で表されている結晶面を示すために用いられているのはこの面指数である。ただし、六方晶系の場合は(hkil)(ただしh+k+i=1)という形で四指数を用いる。
結晶には鉱物が同じでも外形が異なる場合がある。鉱物の組成、原子配列は規則正しくコピーされていても、その結果の結晶の外形が異なるということである。これらは結晶生成時の条件(温度、鉱物の密度など)によって、結晶の成長する方向性が変わってくるため、鉱物種が同一でも結晶面の現れてくる度合いが異なったり、ある結晶面がまったく現れず消滅したりしているものである(逆に結晶生成時の条件が一定ならば同一の外形をとることになる)。つまり、ある鉱物の結晶については、可能な結晶面は決まっているが、状況によってその現われ方が異なり、その組み合わせによって多様な形が現れることになるわけである。したがって、形は変わっても面同士の成す角度は一定であり、この角度を測定することにより結晶の構造を知ることが可能になる(後出の結晶模型はこの作業を行うためのものである)。例えば、黄鉄鉱(Pyrite,FeS2)は正六面体、正八面体、正十二面体の3種の結晶面の組み合わせで、多様な形を取る[図3]。また、水晶(Christal,SiO2)は、天然のものは六角柱状に成長するが、人工的に作ることができるのは四角柱状のものだけである。これは天然の場合と人工の場合とで生成条件が異なるためである。
以上に述べてきた通り、基本となる構造は単純ながらも、結晶は多様な形をとる訳であるが、結晶がこの様な理想的な形となるのは周りにその成長を妨げるものがない空間においてのみである。現実には、何か壁があってそれに沿って平たい形に成長したり、隣の結晶とくっついてしまったりして、その鉱物が本来なるべき理想の結晶形が実現されていない方が多い。だが、このような外界の制約により、意図せざる形になった場合にも、興味深い例がある。最後にこのようなものとして仮像を紹介しよう。 仮像あるいは仮晶(psuedmorph)とは、オリジナルの結晶に対して、別の結晶がその形をコピーしたといえるものである。『地学辞典』(平凡社)によれば、「温度、圧力、化学的状態の変化により、その外形を保ったまま、成分の一部、或いは全部が置換して全く新しい鉱物となったもの」である。結晶A、Bがあるとした場合、結晶A(オリジナルの結晶)の表面に結晶Bが付着して成長したり、或いは結晶Aのあった部分に結晶Bができたりすることにより、結晶Bが結晶Aの形を留めた形になったものをいう。前者のように、結晶の表面を覆って生じた皮殻状のものを包晶仮像、後者の、外形だけを残し、内容物が溶失した後を充填してできたものを充填仮像という。また、元の結晶と仮像との成分の関係によって分類すると、単に分子配列の変化や成分の増減によるものを変質仮像、成分が全く交代され、原鉱物と生成物との間に何らの科学的類似のないものを交代仮像という。 仮像として有名なものには玄能石がある。角錐を2つ合わせたような、両端の尖った石で、柄を外した玄能の形に似ていることからこの名がある。一時はその形から、先史時代の石器ではないかとする向きもあったというが、人類の存在しない第三紀の地層から産するためそれは有り得ない。これは、もとあった結晶がなくなり、その形に方解石(Calcite,CaCO3)の結晶ができているもの、すなわち充填仮像である。形状や組成の類似から、ゲイリュサイト(Gaylussite,Na2Ca(CO3)2・5H2O)、グラウベライト(Glauberite,Na2Ca(SO4)2)等がオリジナルの結晶ではないかとされてきたが、いまひとつしっくりこなかった(玄能石が最大30センチにもなるのに対して、これらにはそれほど大きな結晶が産出しない)。近年、海底の調査が多く行われるようになって、玄能石の新たなオリジナル候補が現れた。それは含水炭酸カルシウムの鉱物イカ石(Ikaite)で、低温の海底で成長する鉱物である。しかし、イカ石をオリジナルとすると、納得の行かない形の玄能石も存在するといい、オリジナルのはっきりしない仮像である(堀秀道著『楽しい鉱物図鑑 2』、草思社、1993年)。 (中村雄紀) |
| 前頁へ | 表紙に戻る | 次頁へ |